高校数学ⅡB 整式の割り算を筆算なし!暗算で解く方法

動画
BGMあり
BGMなし
レベルチェック

まずは、今まで通り筆算で個の割り算の計算をしてみましょう。
従来の筆算

割り算の問題が与えられるともちろん筆算で解きますよね。
でも、時間がかかって仕方がない
文字で筆算するのは苦手
めんどくさい
なんて思っている方に朗報です。
ちょっと式の見方を変えるだけで
筆算を書かずに暗算で答えを求めることができてしまいます。
もちろん、ちょっと頭を使ってもらいます。(笑)
暗算の考え方

割り算の式を見たときに大事になるのが
かけ算に直すということ。
つまり上の画像のように「÷ 」と言う記号を使わずに
かけ算の形に式変形する必要があります。
小学校の時に習った
(割られる数)=(割る数)×(商)
っていう式ですね。
この関係は文字式でも成り立つので
利用してあげましょう。
そうすると、これまで割り算だった式をかけ算として処理することができるわけです。
つまり、先ほどまで、
「割ったらいくらになりますか?」だったのが
「かけて左辺の多項式になるような式を求めよ」
と言う問題に変わったわけです。
いまいちピンとこない人のために👇
例題1

POINTは次数の高い項から考えるということ
この問題では、左辺の2乗の項が最も次数が高いので
掛けて3x^2になるように求めていきます。
右辺を見ると、一つ目の括弧にはxがすでに入っています。
なので、展開したときに3x^2が出てくるためには
xに3xをかけ算すればいいので、
上の画像のようにカッコの中に一つ目の項が入るわけです。

同様に定数項を考えましょう。
左辺の定数項はー2なので、
右辺の一つ目の括弧の中にある定数項の1とかけてー2
になるためには、-2を入れる必要があります。
ですから、上の画像のようになるわけですね。

最後に忘れてはいけないのが、1乗の項です。
最初に2乗の項、次に定数項と考えて、カッコの中に入る式を求めていきました、ですが、まだ1乗の項を確認していません。
ですから、上の画像のように左辺を展開して1乗の項がどうなるかも調べておきましょう。今回はちゃんと左辺と右辺で一致してくれます。
では、なぜ1乗の項を最後に見たのかと言うと、
(余裕がある人はどうぞ)
今回の答えとなる3x-2に秘密があります。
まず、最初の2乗の項に注目して、3xが入ると求めた段階で、その次に続くのは定数項しかありません。
理由は、カッコの中にまず、3xがはいって、次に2次以上の項がはいると、展開したときに2次以上の項が出てきてしまって成り立たなくなるので、
カッコの中に入る次数はどんどん下がっていかないといけないということが分かるので、先に簡単な定数項から見て、最後にややこしい1乗の項を確認したわけです。
例題2

この問題も割り算としてではなく掛け算として考えていきましょう。

まず、左辺の最高次である3次の項から考えていきます。
右辺の一つ目の過去の中にはxが入っています。
ですから、これとかけ算して2x^3を作るには
2x^2が必要だということが分かります。

同様に、2乗の項も見ていきましょう。
右辺を紫の矢印に従って計算すると2乗の項が出てきます。
まずは、すでに決まっている3と2x^2のかけ算(内側の矢印)をすると、
6x^2となります。
左辺では7x^2になっているので、あとx^2が足りませんから、
外側の矢印の計算をしてx^2が出てくるようにせっていすると、
カッコの中にはxが入ることになります。

続いて、定数項です。
左辺の定数項は6ですから、
右辺の3とかけ算して6になるのは2なので、
カッコの中の最後の項が埋まります。

もちろん、1乗の項の確認も忘れずに。
ややこしそうですが、一つ一つの計算に注目するとかけ算とか割り算程度なので、暗算でもできそうですね。
例題3

最後の問題も同様に掛け算で処理します。
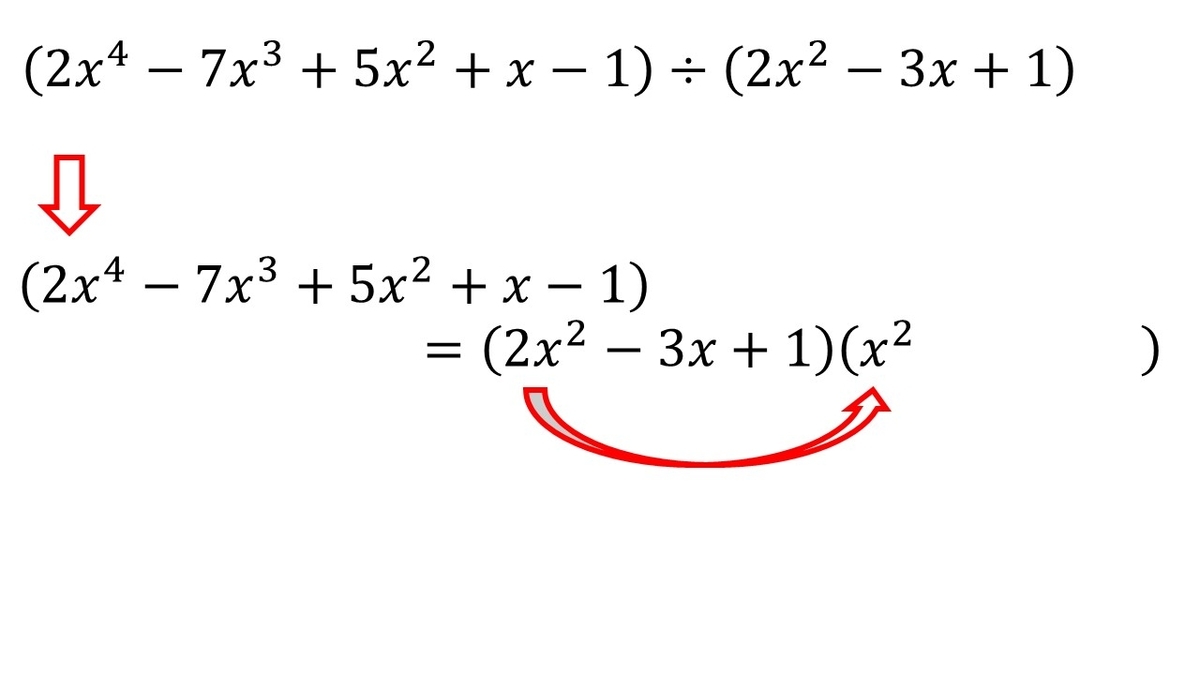
まずは、次数の一番高い4次の項からですね。

続いて3次の項

そして、定数項と言う順にみていきます。
ここでも、右辺のカッコの中が2乗、1乗、ときているので、最後に定数項が来るということが分かりますから、左辺の2乗、1乗の項を飛ばして定数項を確認しているわけです。
もちろん、左辺の2乗、1乗の項と一致するのかも忘れずに確認!

今回はちょとと2乗の項がややこしかったかな~。


おまけ

この割り算どうやって計算します?
筆算かそれとも掛け算として処理するか・・・
実は、この問題が👇のように
因数分解を利用できると気付いたら早いですね。

式の計算問題はこんな感じで、
因数分解とか展開を利用できるので面白いですね。
まとめ

今回紹介してるのはお遊びみたいな方法です。
必ずできないといけないというものではありません。
また、割り算を暗算で処理するのは、
余りが出ないときと分かっているときにしましょう。
余りがあると気にこの方法を使うのは危険が伴います。(笑)
それでは、
さようなら。